중3이 되면 이차방정식과 이차함수를 배우는데 고등학교에 올라가면 둘의 관계에 대해 심도 있게 다룬다 이때 판별식이 결정적인 역할을 하는데 판별식은 이차함수와 x축과의 관계를 나타내는 중요한 열쇠가 된다.
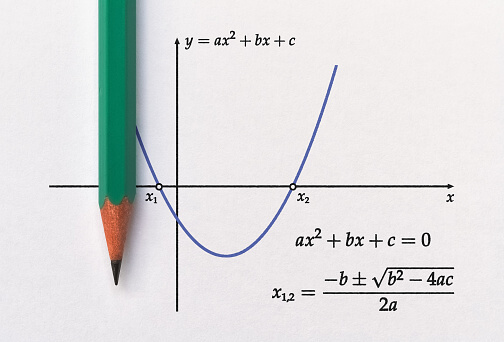
이차방정식과 이차함수의 관계
한마디로 말하면 이차방정식의 근은 이차함수의 x절편이다. 이차방정식의 근은 2개이거나 1개(중근)이거나 0개이다. 근의 개수는 판별식을 이용하여 쉽게 구분할 수 있다. 이차함수를 그리면 함수가 x축과 만나는 교점이 몇 개인지 판단하는 기준이 된다. 이차방정식을 풀었을 때 서로 다른 근이 2개가 존재한다면 그 이차방정식을 y와 x 에관한 함수로 표현한 이차함수는 x축과 두 점에서 만난다. 이차방정식의 근이 1개 (중근)으로 존재한다면 이차함수는 x 축과 접한다. (한 점에서 만난다.) 이차방정식의 실근이 없다면 이차함수는 x축과 만나지 않는다. 이차방정식과 이차함수의 관계를 묻는 문제와 판별식을 어떻게 이용하는지에 대한 문제는 매우 중요하며 빈번하게 출제된다. 이것은 고등학교에 올라가면 이차함수와 일차함수의 관계로 확장하는데 그 내용이 거의 일치한다. 이차함수와 일차함수의 관계식에서 일차함수를 이차함수로 이항 하면 이차함수와 x축과의 관계로 다시 돌아온다. 이 원리를 이해하는 것은 고등학교 과정에서 매우 중요한 일이다.
판별식
판별식은 이차방정식의 실근의 개수가 몇개인지 판단하는 공식이다. 근데 이차방정식의 실근의 개수는 x축과의 교점을 의미하기 때문에 판별식은 이차함수의 x축과의 교점을 판단하는 공식이 된다. 많은 학생들이 판별식을 잘 이해하지 못하고 넘겨버리기 쉽상이고 배우더라도 잘 잊어먹게 된다. 판별식을 기억하는데 도움이 되는 문구 하나를 적어본다면 판별식은 (이차방정식의 실근의 개수를 판별하는 식) 이라고 기억하면 도움이 된다. 판별식은 두 개로 구분되는데 일반공식과 짝수공식으로 b^2-4ac과 b'^2-ac로 표현한다.(이때 b/2 = b') 학생들이 짝수 공식을 이용하는데 불편해하고 낯설어하는 경향이 있는데 판별식을 배울 때 약간 어려움이 따르더라도 확실히 이해하여야 한다. 판별식은 이차함수와 x축과의 관계를 나타내지만 나중에는 이차함수와 일차함수 이외에도 다양한 교점을 파악하는데 쓰이게 된다. 이차방정식, 이차함수, 판별식 이 세 가지의 관계는 매우 밀접하므로 서로 연계하여 꼼꼼히 공부해야 한다.
근의 공식
근의 공식은 이차방정식의 실근을 구하는 공식이다. 이차방정식은 크게 세가지 풀이방법으로 구분된다. 제곱근을 이용한 풀이 , 인수분해를 이용한풀이 , 근의공식을 이용한 풀이이다. 제곱근을 이용한 풀이는 중3때 사용하고 간단한 이차방정식에서 사용되고 대부분은 인수분해를 이용한 풀이를 이용한다. 인수분해를 풀이를 이용한 풀이는 이차방정식이 인수분해가 되어야만 가능한데 만약 인수분해가 되지 않을경우에 근의공식을 사용한다. 근이 공식의 유도과정은 제곱근을 이용한풀이에서 기초된다. 공식을 외울때 도움이 되므로 한번쯤은 유도해보길 바란다. 근의공식의 특징에는 루트안에 판별식이 들어있다는 점이다. 실수는 루트안에 항상 양수이여야한다. 만약 루트안의 연산이 음수가 된다면 실근이 0개인것이고 루트안이 0이된다면 1개의 중근을 갖는 형태가 된다. 루트안이 양수이면 두개의 실근을 갖는데 이는 판별식과 완벽히 동일하다. 근의공식을 외우면서 판별식도 자연스럽게 기억하는 공부방법이 도움이된다. 근의공식은 수능 보는 그날까지 사용된다. 심지어 대학을 졸업하고 30대가 넘어서도 기억하는 사람들이 많다 그 정도로 학창 시절에 많이 사용되므로 외워놓고 시작하는 것이 편안한 학창 시절을 보내는데 도움이 될 것이다.
댓글